数组
链表
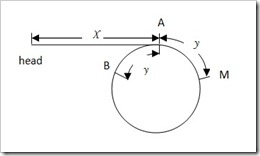
- 判断单链表中是否有环找到环的入口节点
- 使用追赶的方法,设定两个指针slow、fast,从头指针开始,每次分别前进1步、2步。如存在环,则两者相遇;如不存在环,fast遇到NULL退出
- 如何知道环的长度
- 记录下问题1的碰撞点p,slow、fast从该点开始,再次碰撞所走过的操作数就是环的长度s
- 如何找出环的连接点在哪里?
- 碰撞点p到连接点的距离=头指针到连接点的距离,因此,分别从碰撞点、头指针开始走,相遇的那个点就是连接点。
- 假设slow行进了x并在A点进入环路时,fast在环中已经行进了n圈来到B点(n>=0),其行进距离为2x,则可得到如下等式:2x = x +ns+s-y,做一下运算,即x=(n+1)s-y
- 若此时再设置一个指向头节点的指针p,而slow在M处,当p行进了x来到A点时,M行进了x=(n+1)s-y,恰好也来到A处,此时,2个指针相遇了。走的步数即为x长度可知
- 带环链表的长度是多少?
- 问题3中已经求出连接点距离头指针的长度,加上问题2中求出的环的长度,二者之和就是带环单链表的长度
排序
- 快排过程,复杂度,适用条件
复杂度:期望O(nlgn) 最坏O(n^2)
适用条件:待排列基本无序
public class Quick {
public void sort(int[] array){
List<Integer> list = new ArrayList<Integer>();
for (int i = 0; i < array.length; i++) {
list.add(array[i]);
}
//Collections.shuffle()使数组乱序
Collections.shuffle(list);
Iterator<Integer> ite = list.iterator();
int i = 0;
while (ite.hasNext()){
array[i++] = ite.next();
}
sort(array, 0, array.length-1);
}
private static void sort(int[] a, int low, int high) {
if (low >= high){
return;
}
int j = partition(a, low, high);
sort(a, low, j-1);
sort(a, j+1, high);
}
private static int partition(int[] array, int low, int high) {
int last = array[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (array[j] <= last){
i++;
//用异或做交换运算的两个值不能相同
if (i != j){
//(a ^ b) ^ b=a ^ (b ^ b)=a ^0=a
array[i] = array[i]^array[j];
array[j] = array[i]^array[j];
array[i] = array[i]^array[j];
}
}
}
if ((i+1) != high){
array[i+1] = array[i+1]^array[high];
array[high] = array[i+1]^array[high];
array[i+1] = array[i+1]^array[high];
}
return i+1;
}
}
- 二叉平衡树,增删节点
- 完全二叉树
class Node {
public Node leftchild;
public Node rightchild;
public int data;
public Node(int data) {
this.data = data;
}
}
public class TestBinTree {
/**
* 将一个arry数组构建成一个完全二叉树
* @param arr 需要构建的数组
* @return 二叉树的根节点
*/
public Node initBinTree(int[] arr) {
if(arr.length == 1) {
return new Node(arr[0]);
}
List<Node> nodeList = new ArrayList<>();
for(int i = 0; i < arr.length; i++) {
nodeList.add(new Node(arr[i]));
}
int temp = 0;
while(temp <= (arr.length - 2) / 2) {
//注意这里,数组的下标是从零开始的
if(2 * temp + 1 < arr.length) {
nodeList.get(temp).leftchild = nodeList.get(2 * temp + 1);
}
if(2 * temp + 2 < arr.length) {
nodeList.get(temp).rightchild = nodeList.get(2 * temp + 2);
}
temp++;
}
return nodeList.get(0);
}
/**
* 层序遍历二叉树,,并分层打印
* @param root 二叉树根节点
*
*/
public void trivalBinTree(Node root) {
Queue<Node> nodeQueue = new ArrayDeque<>();
nodeQueue.add(root);
Node temp = null;
int currentLevel = 1;
//记录当前层需要打印的节点的数量
int nextLevel = 0;
//记录下一层需要打印的节点的数量
while ((temp = nodeQueue.poll()) != null) {
if (temp.leftchild != null) {
nodeQueue.add(temp.leftchild);
nextLevel++;
}
if (temp.rightchild != null) {
nodeQueue.add(temp.rightchild);
nextLevel++;
}
System.out.print(temp.data + " ");
currentLevel--;
if(currentLevel == 0) {
System.out.println();
currentLevel = nextLevel;
nextLevel = 0;
}
}
}
/**
* 先序遍历
* @param root 二叉树根节点
*/
public void preTrival(Node root) {
if(root == null) {
return;
}
System.out.print(root.data + " ");
preTrival(root.leftchild);
preTrival(root.rightchild);
}
/**
* 中序遍历
* @param root 二叉树根节点
*/
public void midTrival(Node root) {
if(root == null) {
return;
}
midTrival(root.leftchild);
System.out.print(root.data + " ");
midTrival(root.rightchild);
}
/**
* 后序遍历
* @param root 二叉树根节点
*/
public void afterTrival(Node root) {
if(root == null) {
return;
}
afterTrival(root.leftchild);
afterTrival(root.rightchild);
System.out.print(root.data + " ");
}
public static void main(String[] args) {
TestBinTree btree = new TestBinTree();
int[] arr = new int[] {1,2,3,4,5,6,7};
Node root = btree.initBinTree(arr);
System.out.println("层序遍历(分层打印):");
btree.trivalBinTree(root);
System.out.println("\n先序遍历:");
btree.preTrival(root);
System.out.println("\n中序遍历:");
btree.midTrival(root);
System.out.println("\n后序遍历:");
btree.afterTrival(root);
}
}
- 二分查找
- 10000个数找重复
- hashset
- 10001和 减去 10000和
- 一堆数中找和为K的两个数
- 可以用hash表来存储数组中的元素,这样我们取得一个数后,去判断sum - val 在不在数组中,如果在数组中,则找到了一对二元组,它们的和为sum,该算法的缺点就是需要用到一个hash表,增加了空间复杂度。
- 同样是基于查找,我们可以先将数组排序,然后依次取一个数后,在数组中用二分查找,查找sum -val是否存在,如果存在,则找到了一对二元组,它们的和为sum,该方法与上面的方法相比,虽然不用实现一个hash表,也没不需要过多的空间,但是时间多了很多。排序需要O(nLogn),二分查找需要(Logn),查找n次,所以时间复杂度为O(nLogn)。
- 该方法基于第2种思路,但是进行了优化,在时间复杂度和空间复杂度是一种折中,但是算法的简单直观、易于理解。首先将数组排序,然后用两个指向数组的指针,一个从前往后扫描,一个从后往前扫描,记为first和last,如果 fist + last < sum 则将fist向前移动,如果fist + last > sum,则last向后移动。
字符串
栈
树
分治
回溯
哈希
复杂度
动态规划
1、思考状态
状态先尝试“题目问什么,就把什么设置为状态”。然后考虑“状态如何转移”,如果“状态转移方程”不容易得到,尝试修改定义,目的仍然是为了方便得到“状态转移方程”。
2、思考状态转移方程(核心、难点)
状态转移方程是非常重要的,是动态规划的核心,也是难点,起到承上启下的作用。
技巧是分类讨论。对状态空间进行分类,思考最优子结构到底是什么。即大问题的最优解如何由小问题的最优解得到。
归纳“状态转移方程”是一个很灵活的事情,得具体问题具体分析,除了掌握经典的动态规划问题以外,还需要多做题。如果是针对面试,请自行把握难度,我个人觉得掌握常见问题的动态规划解法,明白动态规划的本质就是打表格,从一个小规模问题出发,逐步得到大问题的解,并记录过程。动态规划依然是“空间换时间”思想的体现。
3、思考初始化
初始化是非常重要的,一步错,步步错,初始化状态一定要设置对,才可能得到正确的结果。
-
角度 1:直接从状态的语义出发;
-
角度 2:如果状态的语义不好思考,就考虑“状态转移方程”的边界需要什么样初始化的条件;
-
角度 3:从“状态转移方程”方程的下标看是否需要多设置一行、一列表示“哨兵”,这样可以避免一些边界的讨论,使得代码变得比较短。
4、思考输出
有些时候是最后一个状态,有些时候可能会综合所有计算过的状态。
5、思考状态压缩
“状态压缩”会使得代码难于理解,初学的时候可以不一步到位。先把代码写正确,然后再思考状态压缩。
状态压缩在有一种情况下是很有必要的,那就是状态空间非常庞大的时候(处理海量数据),此时空间不够用,就必须状态压缩。
Leetcode [5] 最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
*
* 示例 1:
* 输入: "babad"
* 输出: "bab"
* 注意: "aba" 也是一个有效答案。
* 示例 2:
* 输入: "cbbd"
* 输出: "bb"
这道题比较烦人的是判断回文子串。因此需要一种能够快速判断原字符串的所有子串是否是回文子串的方法,于是想到了“动态规划”。
“动态规划”最关键的步骤是想清楚“状态如何转移”,事实上,“回文”是天然具有“状态转移”性质的:
一个回文去掉两头以后,剩下的部分依然是回文(这里暂不讨论边界)。
依然从回文串的定义展开讨论:
1、如果一个字符串的头尾两个字符都不相等,那么这个字符串一定不是回文串;
2、如果一个字符串的头尾两个字符相等,才有必要继续判断下去。
(1)如果里面的子串是回文,整体就是回文串;
(2)如果里面的子串不是回文串,整体就不是回文串。
即在头尾字符相等的情况下,里面子串的回文性质据定了整个子串的回文性质,这就是状态转移。因此可以把“状态”定义为原字符串的一个子串是否为回文子串。
第 1 步:定义状态
dp[i][j] 表示子串 s[i, j] 是否为回文子串。
第 2 步:思考状态转移方程 这一步在做分类讨论(根据头尾字符是否相等),根据上面的分析得到:
dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]
分析这个状态转移方程:
(1)“动态规划”事实上是在填一张二维表格,i 和 j 的关系是 i <= j ,因此,只需要填这张表的上半部分;
(2)看到 dp[i + 1][j - 1] 就得考虑边界情况。
边界条件是:表达式 [i + 1, j - 1] 不构成区间,即长度严格小于 2,即 j - 1 - (i + 1) + 1 < 2 ,整理得 j - i < 3。
这个结论很显然:当子串 s[i, j] 的长度等于 2 或者等于 3 的时候,我其实只需要判断一下头尾两个字符是否相等就可以直接下结论了。
如果子串 s[i + 1, j - 1] 只有 1 个字符,即去掉两头,剩下中间部分只有 11 个字符,当然是回文;
如果子串 s[i + 1, j - 1] 为空串,那么子串 s[i, j] 一定是回文子串。
因此,在 s[i] == s[j] 成立和 j - i < 3 的前提下,直接可以下结论,dp[i][j] = true,否则才执行状态转移。
(这一段看晕的朋友,直接看代码吧。我写晕了,车轱辘话来回说。)
第 3 步:考虑初始化
初始化的时候,单个字符一定是回文串,因此把对角线先初始化为 1,即 dp[i][i] = 1 。
事实上,初始化的部分都可以省去。因为只有一个字符的时候一定是回文,dp[i][i] 根本不会被其它状态值所参考。
第 4 步:考虑输出
只要一得到 dp[i][j] = true,就记录子串的长度和起始位置,没有必要截取,因为截取字符串也要消耗性能,记录此时的回文子串的“起始位置”和“回文长度”即可。
第 5 步:考虑状态是否可以压缩 因为在填表的过程中,只参考了左下方的数值。事实上可以压缩,但会增加一些判断语句,增加代码编写和理解的难度,丢失可读性。在这里不做状态压缩。
下面是编码的时候要注意的事项:总是先得到小子串的回文判定,然后大子串才能参考小子串的判断结果。
思路是:
1、在子串右边界 j 逐渐扩大的过程中,枚举左边界可能出现的位置;
2、左边界枚举的时候可以从小到大,也可以从大到小。
贪心算法
小技巧
没有辅助堆栈 / 数组的帮助下 “弹出” 和 “推入” 数字
这种方法有点危险,因为当 text{temp} = text{rev} cdot 10 + text{pop}temp=rev⋅10+pop 时会导致溢出int最大值是2147483647,最小值是-2147483648 -> [−2^31, 2^31 − 1]
//pop operation:
pop = x % 10; //取末尾数字,读操作
x /= 10; //去除末尾数字,写操作
//push operation:
temp = rev * 10 + pop; //进位,写操作
rev = temp; //数字更新,写操作
回溯
递归和DP怎么区分
递归一般是方法跳进方法里
public string digui(){
digui();
}
DP一般是依赖子结果
public string DP(){
for(){
dp[i] = dp[i - 1] + dp[i - 2];
}
}

